Case 07: Walking in a square
Introduction
This course aims to guide students to make a walking in a square case and review the relevant knowledge of encoder motors and gyroscopes.
Teaching objectives
Learn to use Makecode software to create a program to control the driving route of the car.
Teaching preparation
Before starting teaching, please make sure you have prepared the following necessary materials:
| Picture | Name | Number | Note |
|---|---|---|---|
 | TPbot Edu | 1 | |
 | USB Cable | 1 | |
 | micro:bit | 1 | Prepare Yourself |
 | PC | 1 | Prepare Yourself |
Course Introduction
Hello everyone! Welcome to this new course full of fun and challenges. Today, we will explore how to use programming to control the car and let it complete a preset route task on a special map. This is not only a programming exercise, but also a challenge of logical thinking and strategic planning.
Course Background We have a map consisting of 6 grids, each grid is a 20cm square grid. This map will become the stage for our car's adventure. Your task is to write a program to let the car move from one grid to another along the preset route until the entire task is completed.
Exploration Activities
Understanding the coordinate system: How to determine the position of the car on the map. Programming logic: How to write a program to let the car move along a specified route. Debugging and testing: How to test and adjust your program to ensure that the car can successfully complete the task.
Software
Programming
Click Advanced in the code drawer of MakeCode to view more code options.

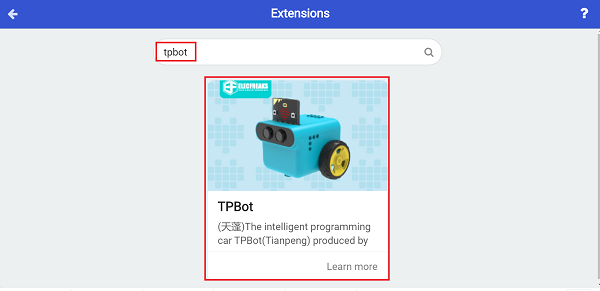
In order to program TPbot Edu, we need to add an extension library. Find Extensions at the bottom of the code drawer and click it. A dialog box will pop up, search for tpbot, and then click to download this code library.
Sample Program
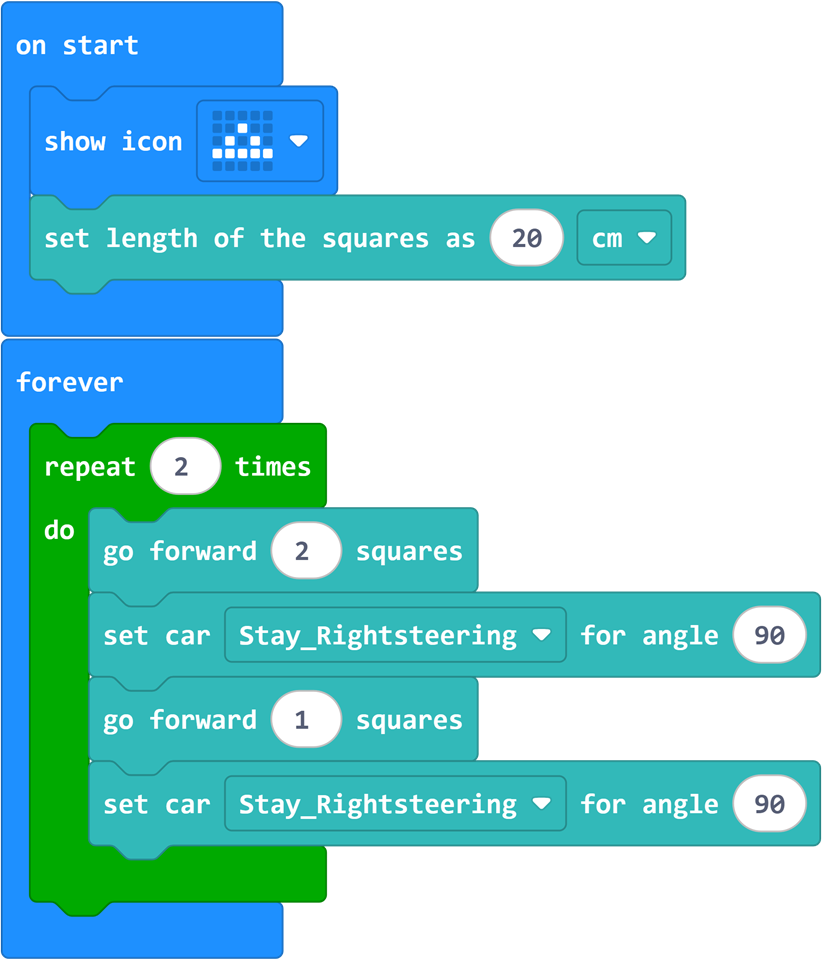
Program
Please refer to the program link: https://makecode.microbit.org/_8tW9Y0c25TDH
You can also download the program directly from the following website.
Conclusion
When turned on, the car drives along the predetermined route.
Extended knowledge
Coordinate system
A coordinate system is a method used in mathematics and physics to determine the position of a point in space. The following is a brief introduction to the basic knowledge of coordinates:
One-dimensional coordinate system (number axis)
The simplest coordinate system is one-dimensional, usually represented by a straight line, called a number axis.
On the number axis, each point has a numerical coordinate, which can be positive, negative, or zero.
The positive direction on the number axis is usually to the right and the negative direction is to the left.
Two-dimensional coordinate system (plane rectangular coordinate system)
The two-dimensional coordinate system extends the one-dimensional system and allows us to determine the position of a point on a plane.
It consists of two mutually perpendicular number axes, usually called the x-axis (horizontal) and the y-axis (vertical).
The point where these two axes intersect is called the origin, and its coordinates are (0, 0).
A point on any plane can be determined by a pair of numerical coordinates (x, y), where x represents the horizontal position and y represents the vertical position. Three-dimensional coordinate system (Cartesian coordinate system in space) The three-dimensional coordinate system further extends the two-dimensional system, allowing us to determine the position of points in three-dimensional space. It consists of three mutually perpendicular axes, usually called the x-axis, y-axis, and z-axis. The point where these three axes intersect is also the origin, and its coordinates are (0, 0, 0). Any point in space can be determined by three numerical coordinates (x, y, z), where x, y, and z represent the position of the point on the three axes respectively. Representation of coordinates In a coordinate system, coordinates are usually represented in the form of ordered pairs or ordered triplets. For example, in a two-dimensional coordinate system, the coordinates of point A can be represented as (3, 4), indicating that point A is 3 units away from the origin on the x-axis and 4 units away from the origin on the y-axis. In a three-dimensional coordinate system, the coordinates of point B can be expressed as (2, 5, -1), which means that point B is 2 units away from the origin on the x-axis, 5 units away from the origin on the y-axis, and 1 unit away from the origin on the z-axis. Application of coordinates Coordinate systems are widely used in mathematics, physics, engineering, computer graphics and other fields. In map making and navigation, coordinate systems are used to determine geographic locations. In computer graphics and game development, coordinate systems are used to determine the position of objects on the screen. Understanding coordinate systems is the basis for understanding more complex mathematical concepts and participating in many scientific and technological activities.